日期:2025-06-23 10:05:22
|作者:沈顺清冠盈配资
(香港大学物理系)
本文选自《物理》2025年第5期
1米—千克—秒的演变
你知道现在用来测量长度和质量的单位,米和千克,是怎么来的吗?其实,它们最早起源于1799年法国巴黎人创立的公制系统。巴黎人将从北极经过巴黎到赤道的子午线的长度分成一千万份,并把每份的长度定义为一米;然后再将一米分成十份,每份的长度就是分米,从而形成了十进制的长度单位。以长度单位为基础,进一步可以定义面积和容量的单位。他们将每立方分米在4℃时蒸馏水的质量定为一千克。以此为标准,用铂金制作了两个标准器件,作为长度和质量的标准原器(图1),这样就有了大家都可以共同参考的计量标准。而时间是根据每一天作为标准,把一天分成24小时,每小时60分,每分钟60秒。换句话说,时间单位秒被定义为每天的86400分之一。如此,我们就有了米—千克—秒的公制系统。地球的子午线长度原则上是大家都能独立测量的,蒸馏水也是很容易取得的,这一标准的制定体现了一个普适的计量原则:“在任何时间,对任何人”都适用。

图1 (a)法国巴黎的公共标准长度米;(b)建于1791年和存放在巴黎的国际千克原器(取自网络)
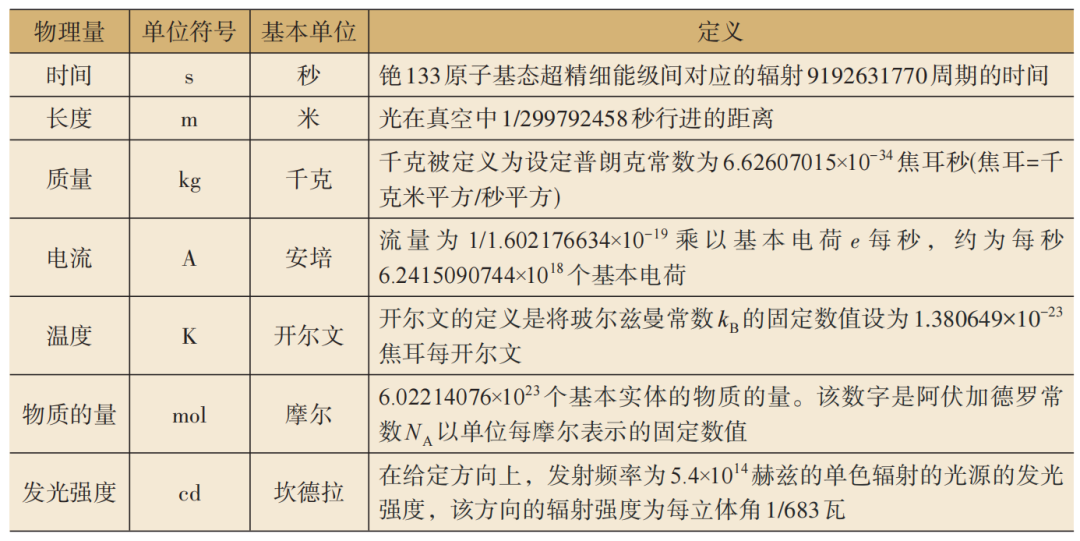
1875年,有17个国家和相关组织在巴黎签订了一个公约,确定了以米和千克为标准单位,以组织形式广泛推动公制,成为大家共同使用的度量衡单位。这方便了人们日常生活中的计量,也让不同地区之间的商业交流更加便利。1889年,在新成立的第一届国际计量大会(CGPM)上又引入了时间秒,形成了米—千克—秒系统,推动和建立统一的国际计量标准。1954年,第十届国际计量大会又加入了3个新的单位,安培(电流的单位)、开尔文(温度的单位)和坎德拉(亮度的单位),扩大了标准单位的应用范围。1960年,该组织正式命名了国际标准单位制(SI),包括米、千克、秒、安培、开尔文和坎德拉6个基本单位,使它能在不同学科和领域统一使用。并且首次利用氪原子光谱的波长来重新定义长度米,用物理常数替代实物标准原器,这是十分重要的一步,能使我们更精确地测量各种物理量,适应科技的快速发展。1967年,又采用铯原子的光谱频率重新定义了秒。到1983年,进一步利用真空中的光速为常数,取代氪原子光谱的波长,再次重新定义了长度米。这样,国际标准单位制逐渐从以实物原器为标准,过渡到以物理学基本常数为基础的单位制,它提供了普适而严格的计量标准,大大提高了测量的精度。2018年,第二十六届国际计量大会决定选定7个物理基本常数(表1)[1],并以此为基础导出了7个物理基本量的基本单位(表2)[1],完全取代实物标准原器作为标准单位,这个改革从2019年5月开始实施。这些量的重新定义,虽然对人们日常生活和商业活动影响并不大,但为科学研究和高科技发展提供了坚实的基础。
表1 7个基本常数、符号和 定 义[1]
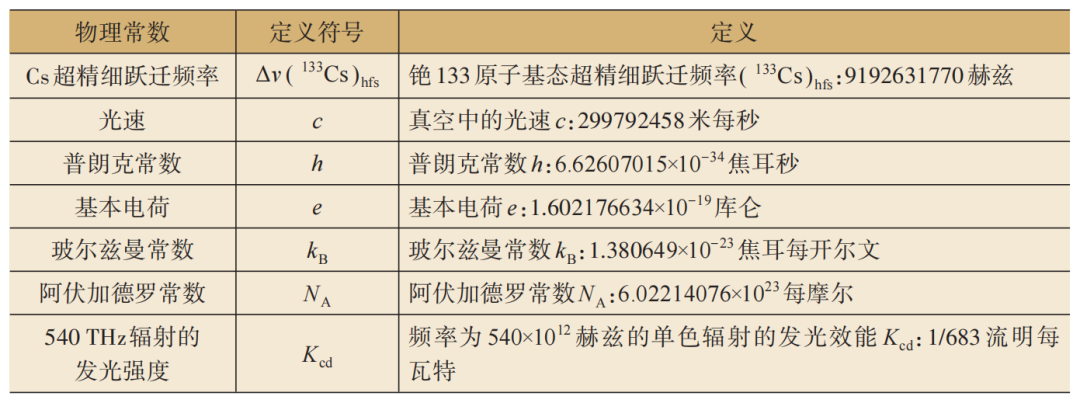
表2 7个基本量、单位符号、基本单位和定义[1]
2基本物理常数选择
国际标准单位制中选用的物理常数是在数学物理方程中出现的有量纲的系数。物理常数的出现是现代科学发展的一个重要组成部分。例如牛顿力学中,两个物体间吸引相互作用中的万有引力常数
G,以及光在真空中的传输速度c,它们不依赖于运动坐标系,并且不会随时间和地点变化,适用于所有的观测者,是普适的常量。由于物理常数本身带有量纲,人们可以将它作为一种普适的计量标准。例如真空中的光速有速度的量纲,可以用作速度的自然标准单位。在实践活动中,利用物理常数来定义物理量的单位,在不同的学科中都有应用。像在天文学中采用的长度单位光年,是指光在一年时间传播的距离,相对于日常生活,这是一个极大的长度单位。因此作为标准单位的物理基本常数的选择并不是唯一的,但它同时必须是完备和非冗余的。如果在实际运用中被选作为标准,这些基本常数就要求可以被精确测量,以满足实际需求。
最初以地球子午线长度来定义的米,就是以地球的尺度大小作为物理常数。这个定义引起的偏差主要来自两个方面,一是实际测量过程中带来的不确定性,二是地球本身并非一个表面理想光滑的球体,表面的不规则性也会带来偏差。两方面都给米的定义带来了不可避免的局限性。作为单位标准,在众多的物理常数中,主要利用能量
E相关的等价关系进行关联:
Emc2 =hνeVkBT
这组方程很好地总结了几个物理常数和相应物理量之间的相互关联,是现代物理学中最基础的结论[2],为我们提供了参考标准。其中普朗克常数
h、光速c、基本电荷e和玻尔兹曼常数kB 是基本的物理常数,它们都具有一定量纲,而且现代技术也能为这些参量提供实际可行的测量方法。m是质量,是频率,V是电压,T是温度,它们是相对应的物理可观测量。相对论中的质量和能量关系Emc2 ,由于c是物理常数,能量和质量就直接联系起来,可以相互转换;量子物理中能量和频率的关系Ehν,频率是时间的倒数,这样能量和时间就关联在一起;电磁场论中的EeV,把能量和电压直接联系在一起;热力学关系EkBT给出了能量和温度的关系。这组方程实际上总结了相对论、量子科学、电磁学和热力学几个不同学科的知识,形成了国际标准单位制的科学基础。从这几个物理量中,挑选任何一个量作为标准,能量的大小就可确定,进而相应其他的量也就都可确定了。我们选定了铯原子Cs超精细跃迁频率ΔCs 作为基本频率标准,其他的量,像质量、电压和温度的单位,就都可利用相对应的基本常数来一一确定。
因此,选定光速
c、普朗克常数h、基本电荷e和玻尔兹曼常数kB 为有量纲的基本常数后,加上基本频率基准ΔCs ,我们就可确定质量、时间、电流和温度的单位大小了。这样,国际标准单位制就有了科学的基础,可以满足人们的实际需求。
3秒与米
物理意义上的时间定义源于物体的周期运动,如每天的太阳升起和落下,我们就有了一“天”的时间概念,又以太阳在天空的位置,再把一天细分成十二个时辰(图2)。又例如单摆在重力下的周期运动,也可以用来定义时间的单位。新的时间定义是基于现代原子物理和冷原子技术的飞速发展,利用原子光谱中非常稳定的频率作为时间的参考标准。我们选定的铯原子(Cs)133,它的外壳层只有一个
s电子,自旋是1/2,它原子核的自旋是7/2。电子自旋和原子核间的超精细相互作用导致有两个不同的能级,一个是电子自旋和原子核自旋平行的态,总自旋为4;另一个是电子自旋和原子核自旋反平行的态,总自旋为3。总自旋为4的态能量略高于自旋为3的态。当电子从自旋为4的态跃迁到自旋为3的态,辐射出的光子频率为ΔCs =9192631770赫兹,利用光速cCs ,可以导出相应的波长为3.26厘米,长度在微波的波长范围内。这个频率非常稳定,是被选定为基本频率标准的原因之一。频率的量纲是时间的倒数,然而这个频率对应的时间周期太短,所以一秒被定义为9192631770个辐射周期,即9192631770/ΔCs 。这个9位数的选取只是为了所定义的秒足够接近人们通常小时—分—秒中所定义的时间长度,没有其他特别的含义。
图2 利用日影测量时间的日晷(a)和单摆座钟(b)(取自网络)
原子钟是基于原子系统的一种钟表。铯原子可以处于两种可能的低能态之一,处于一种能态的铯原子受到微波辐射作用,电子被激发,有机会跃迁到另一个能态。辐射的频率越接近原子固有振荡频率,转换状态的原子数量就越多,这种相关性允许对微波辐射的频率进行非常精确的调节。一旦微波辐射被调节到已知频率,使得最多数量的原子转换状态,该原子及其相关的转换频率就可以用作计量时间的基准振荡器。为了提高测量的精确度,通常会要求原子钟在极低温下运行,以减少原子运动对测量的影响。选择铯原子作为基准是因为铯原子较重,在相同温度下,它的运动速度相比其他原子要低得多,这样可以减少热运动带来的相对误差。
光速
c是个普适的基本常数。在经典电磁场理论中,光是交变电磁场形成的电磁波,在真空中传播,传播速度由真空介电常数0 和磁导率0 来决定。从描写电磁场变化的麦克斯韦方程可以发现,光速 不依赖于运动坐标系。在现代量子论中,光由没有静质量的光子组成,光子是电磁场的基本元激发,它的运动速度就是光速c,这是物质运动的极限。光速不变原理是狭义相对论的基础,也是现代时空观的基础。当然,在通常的介质中,如水中,光速会变慢,但它在真空中的速度是恒定的。现在真空中的光速c被严格定义为299792458米每秒,约30万公里每秒。光从地球到月球需要大约1.25秒。光速等于波长乘以频率,或波长除以时间周期,波长是有长度量纲的。1960年,国际标准单位制曾以氪原子光谱中的波长来定义长度单位,所以作为常数的光速c实际上为长度和时间提供了一个换算基准,长度和时间可以互换。有了标准时间秒后,一米就是光在1/299792458秒的时间里走过的长度,这样我们确定了长度单位米。
光速
c和铯原子超精细跃迁频率ΔCs 决定了时间和长度的单位。这得益于激光和冷原子技术的发展,使我们有非常精确的时间和长度的测量标准。
4千克与安培冠盈配资
用来衡量物体质量的单位是千克,用来衡量电流强度的单位是安培。这两个单位都与两个重要的物理常数有关,即普朗克常数
h和基本电荷e。普朗克常数h是1900年 德国物理学家马克斯·普朗克(图3)在研究黑体辐射时提出的。理想的黑体是不透明和无反射的物体,在它与环境处于热力学平衡的状态下,会向周围发射电磁波。在自然界中,宇宙背景就是一个温度为2.7开尔文的理想黑体辐射体。为拟合电磁波的热辐射强度的实验观测数据,普朗克提出了以他名字命名的公式:

图3 德国物理学家马克斯·普朗克(1858—1947),普朗克常数
h的发现者(取自:NobelPrize.org)
普朗克公式可在不同温度下从低频到高频区域完美地拟合实验测量结果(图4)。在这个公式中,普朗克同时引进了两个与能量相关的常数:普朗克常数
h乘以频率hν具有能量量纲;玻尔兹曼常数kB 乘以温度TkBT也具有能量量纲。这个公式是量子论诞生之前发现的,被后来发展的理论证明是严格的,它在量子论和量子力学的发展过程中起了重要的作用。爱因斯坦首先把hν理解为光量子的能量,用来解释光电效应,这是量子论发展过程中的重要一步。丹麦物理学家尼尔斯·玻尔创造性地把原子光谱和原子能级联系到一起,建立了原子模型。法国物理学家德布罗意将光子具有的波长和频率的概念推广到是所有粒子都具有的一个基本特性,使之成为量子论的基础。量子力学诞生后,普朗克常数作为基本常数,出现在量子力学的各种基本方程中,如位置与动量的基本对易关系和薛定谔方程等。在选定光速c和铯原子超精细跃迁频率ΔCs 后,由普朗克—爱因斯坦能量关系,单个铯原子超精细跃迁频率ΔCs 的光子的能量EhCs ,进一步由爱因斯坦质量与能量关系Emc2 ,可以得到单个光子的有效质量mhCs /c2 。这样,要确定质量的单位,就需要确定普朗克常数h的数值。普朗克常数h最初由黑体辐射的实验数据估算出来。考虑到铯原子的基本标准频率ΔCs ,单个基本标准频率光子对应的质量mhCs /c2 为7.036×10 -41 千克。这其实是个非常小的量,但同时也揭示了质量与普朗克常数是直接联系在一起的。
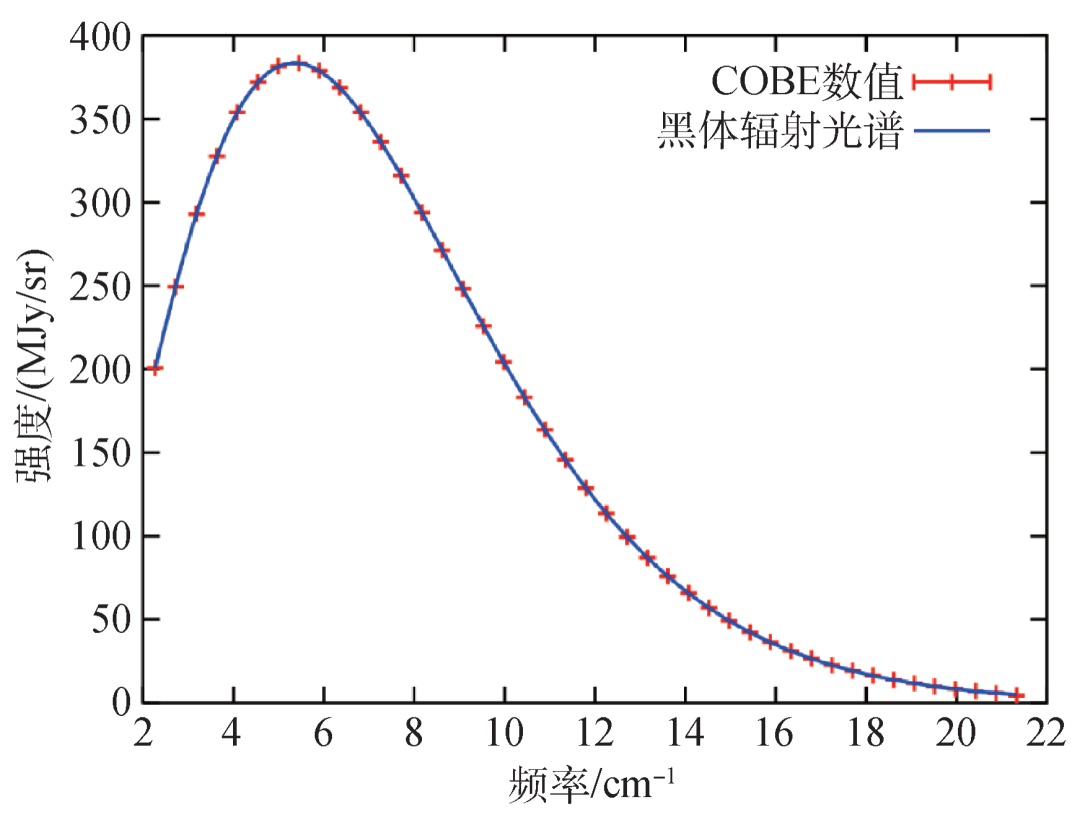
图4 宇宙微波背景(COBE)光谱和 2.725 开尔文黑体辐射光谱的比较:观测的数值和公式的结果完全一致
另一个基本常数是基本电荷
e。现代物理的一个重要结论是物质由原子组成,而原子由电子、中子和质子组成。电子带有负的基本电荷-e,而质子带有正的基本电荷+e。一个基本原则是任何粒子的电荷都是基本电荷的整数倍,不存在非整数电荷的粒子,这就是所谓的电荷量子化原理,也是基本电荷这个术语的含义。基本电荷e最早于1909年用所谓的“油滴实验”测量出来,和现在的标准值只差大约0.6%。有了基本电荷这个概念,加上秒已被定义,我们就可以定义电流的单位安培:即单位时间内流过的电荷量是基本电荷e的1/1.602176634×10 -1 9 倍,约为6.2415090744×10 18 个基本电荷。原有的定义是基于1安培的恒定电流,若在两根长度无限、横截面积可忽略不计的圆形平行直导体中,并且在真空中相距一米,则这两根导体之间将产生的力为每米2×10 -7 牛顿。这个定义强调的是具体的可操作性,而新的定义依赖于电荷的定义和测量。电荷e乘以电压V具有能量的量纲,其实电压的单位同时也确定了,一个伏特为焦耳每库仑。国际标准单位制中选择电流单位安培作为基本单位,而不是电压的单位伏特,其实任取其一都是可以的。
5普朗克常数h和基本电荷e的精确值
基本电荷
e和普朗克常数h的数值最终由两个宏观量子效应来确定,它们分别是超导体间的约瑟夫森效应和整数量子霍尔效应,这是一个非常意外但又优美的结果。每个物理效应中出现了一个物理量,可以用非常高的精度来测量,所以被物理学家用来定义了两个重要的物理常数。这为完成由物理常数确定度量衡单位迈出了非常关键的一步。
约瑟夫森效应是发生在两个弱连接的超导体间的量子隧穿效应。超导电性指某些金属体在极低温下,电阻突然完全消失,且具有完全抗磁性。低温下的电子具有特殊的相位相干性,结合起来展现出宏观量子效应。1962年,年仅22岁的研究生,英国物理学家约瑟夫森(图5)提出,当两个超导体被一个绝缘体分隔开后,超导电子相位的相干性会导致电子穿过势垒形成隧穿电流,并得到了实验的证实。这是个纯量子效应,在经典物理中是不可能发生的。当两个超导体间的电势差为
V时,隧穿电流会随时间波动tc sin(KJVt0 ),其中约瑟夫森常数KJ =2eh0 为两者间的相位差。这个交流约瑟夫森效应的电流振荡频率为fKJV。由于频率测量的相对精度可以高达10 -10 以上,所以约瑟夫森结可以作为一个理想的电压V与频率f的标准转换器。

图5 英国物理学家布赖恩·约 瑟夫森(1940— ),约瑟夫森效应发现者(取自:NobelPrize.org),
KJ =2eh被称 为约瑟夫森常数
n为一个整数值, 是冯·克利青常数。这是个拓扑量子效应,量子化霍尔电阻极其稳定,与样品不规则的形状无关,样品中的杂质和各种相互作用对它也没有影响,实际测量精度可高达10 -9 以上。目前在单层石墨烯和其他二维材料,以及无磁场的铁磁材料中也能观测到这个效应,是个极其理想的电阻标准。有了标准电阻,电流和电压就可以直接转换了。

图6 德国物理学家克劳斯·冯·克利青(1943— ),整数量子霍尔效应的发现者(取自:NobelPrize.org),被称为冯·克利青常数
2018年第28届国际计量大会选定约瑟夫森常数
KJ 和冯·克利青常数RK 为严格物理常数,用以等价地定义基本电荷e和普朗克常数h的精确值。它们之间的关系为基本电荷eRKKJ ),普朗克常数hRKKJ2)。这样两个可测量的物理量和两个基本物理常数就密切地联系在一起了。
6质量的测量
约瑟夫森效应和量子霍尔效应为精确测量质量提供了切实可行的途径。有了精确定义的普朗克常数
h,直接由它给出的单个铯原子标准频率的光子有效质量太小,无法直接运用。实际操作中,测量物体质量使用的是基布尔(Kibble)天秤。它利用了电力和机械动力的平衡,可以精确测量物体质量。这个天秤有两个模式,一是称重模式,利用线圈中的电流在圆形磁场B下的洛伦兹力IBL与重力mg达到平衡mgIBL;另一个模式是速度模式,当线圈在磁场下以均匀速度v运动,法拉第效应会在线圈中产生电压VvBL,其中L为线圈长度,这样样品的质量 。由于电流乘以电压是功率的量纲,单位为瓦特,基布尔天秤又称为瓦特天秤。它原是利用标准质量来测量普朗克常数的,当普朗克常数被定义为基本常数后,这个天秤就反过来用来测量物体的质量了。物体的速度v和重力加速度g都可利用激光技术精确测量,例如重力加速度g可以用原子干涉绝对重力仪来测量 [3] 。电流利用量子霍尔效应转换成电压,VH =RH,而电压可利用约瑟夫森效应进一步转换成频率的测量,fH =KJVH ,和fV =KJV。两个频率fH 和fV 极高的测量精度确保了质量的测量精度。美国国家标准与技术研究所利用这种装置,测量的质量相对精度可达2.0×10 -8 。这个装置实现了由物理常数决定物体质量的实体测量。
7新单位制下的新物理问题
在新单位制下,选定了一些物理常数作为基础。但实际上还有其他物理常数可以选择,如万有引力常数。万有引力常数
G是现代物理学中最早发现的物理常数之一,它出现在牛顿的万有引力定律和爱因斯坦的广义相对论中,也被称为重力常数。万有引力常数的测量,最早由英国物理学家卡文迪什在1797年完成,基于万有引力常数,结合地球的半径Re 和表面重力加速度g,可以导出地球的质量Me =Re 2gG。 当卡文迪什完成万有引力常数的测量后,自然就导出了地球的质量,所以他也被称为最先测量出地球质量的人。从量纲分析的角度来看,G和其他常数一起可以作为质量单位的定义标准。像普朗克单位制中,就是选定Gc、ℏ(=h/2π)和kB为基本常数,从而有时间单位 =5.391×10-44秒,长度单位 =1.616×10-35米和质量单位 =2.176×10-8千克。这些量也曾被认为是时间、长度和质量的最小单位。不过实际测量中G的不确定度大约只有10-5,这限制了千克定义的可重现度。G本应该是取代铯原子频率ΔCs的一个基本常数,因为其测量精度不够高,没有入选为国际单位制的基本常数。在新的单位制下,G变成了一个可导出量,由基本常数来表示。这样就引申出了一个基本的物理问题,即万有引力常数是否可以从理论上推导出来。从量纲分析来看,它必须和光速、普朗克常数相关,Gc5/h(ΔCs)2。而普朗克常数h是量子力学中的基本常数,这是否预示着引力与量子力学是紧密联系在一起的?怎样能从理论上推导出引力常数就变成了一个有待解决的问题。
精细结构常数
,也被称为索末菲常数,是物理学中一个谜一样的无量纲常数,它可以用来量化电磁相互作用的强度。是两个独立能量的比值:距离为的两个电子间的库仑排斥势能和波长为=2π的单光子能量之比, 。≈1/137.035999,它的测量精度在过去百余年来一直在提高。在新的国际单位制下,取决于0 是否随时间演化,换句话说,取决于0 = 是否是一个常数。光速不变原理只确定了0 和0 的乘积是常数,而它们比值是否为常数,是一个值得进一步探讨的基本问题。当然,怎样从理论上推导出精细结构常数0 也是个有趣的问题。从这个常数发现至今已有一百多年,有不少著名的物理学家都试图理解它,随着各种物理量测量精度的不断提高,我们或许可以对这个数有更深刻的认识。
当然,物理学中还有许多其他常数,它们是否为独立的常数,都是物理学的最基本问题。一旦我们接受了国际单位制,或任何物理常数定义的单位制,所有其他的物理常数应该都是可推导量。比如说,电子和质子的质量比值约为1/1836,也是个无量纲常数。
8凝聚态物理学与精密测量
早期的凝聚态物理学,也就是我们通常说的固体物理,按泡利(Wolfgang Pauli)说法,是脏的物理学(Festkörperphysik ist eine Schmutzphysik);盖尔曼(Murray Gel-Mann)则将固态(solid state)称之为肮脏状态(squalid state),与核物理或粒子物理相比,认为固体物理学是平庸且缺乏深度的。人们很难想象它会和精密测量有联系。凝聚态物理学所研究的物质是由许多成分组成的,这些成分之间都有很强的相互作用和很多不确定的因素,这使整个领域的研究变得复杂而且困难。人们很难得到一个理想简单的系统,将其看成一个“肮脏的状态”也是自然的。然而,正是这些复杂的相互作用,当系统的粒子数量极大时,从量变到质变,会出现一系列奇特的量子相干状态,比如超导电性、铁磁和反铁磁相以及量子霍尔效应等,这些物态有其独特的宏观物理性质。像超导体中的零电阻,电子在超导态中的运动完全不受原子核和其他杂质的任何干扰,可以毫无阻力地自由穿行,众多电子因彼此间的相互作用,抱团形成一种超流动状态。量子相干的尺度远远大于原子间的距离和各种缺陷尺度,表现出的物理性质远超出了人们的想象。
约瑟夫森效应和量子霍尔效应实际上源于凝聚态物理中的两类不同的量子物态。一个是源于由短程相互作用引发的长程有序的物态,是多体系统中一种特有的层展现象。另一个是固体晶格能带结构和拓扑学相结合的产物,有极其特殊的稳定性,不受杂质和多体相互作用的影响。对应的约瑟夫森常数和冯·克利青常数是这两种不同量子物态所呈现的产物。所以,尽管凝聚态物理学可能看起来“脏”,但它却能产生非常纯净、精确的物理常数,这是非常神奇的。所谓出淤泥而不染,是自然界的常见现象,也会出现在凝聚态物理学中。
9其他几个量
国际标准单位制中选定的7个基本常数,还有两个量和温度与亮度有关,它们分别是玻尔兹曼常数
kB 和发光效率Kcd。玻尔兹曼常数kB和是和温度T密切联系在一起的一个基本常数,来自热力学与统计力学。在理想气体中,体积为VN个粒子的气体压强pNkBTV,而气体中单个理想粒子的平均能量是 。作为最后一个确定的基本常数,其精确值的确定,历经多年努力,最终通过声学气体测温法获得。这种方法利用微波和声学共振确定三轴椭球室中单原子气体的声速,实验相对精度高达10-10。在实际应用中,玻尔兹曼常数使用了足够多的精确数字,以确保273.16开尔文具有足够多的有效数字来包含水三相点的不确定性,并且水在273.00开尔文,也就是摄氏零度时仍会以高精度正常结冰。在选择玻尔兹曼常数为基本常数之前,水的三相点精确值是273.16 K,现在,这种不确定性就转移到水的三相点上了,目前它的数值为273.1600(1)开尔文,在小数点后第五位数才出现细微的差别。不过,物理上kBT总是一起出现的,这使kB不同于其他几个物理常数。目前,我们还没有一个普适物理关系式在任何温区成立,特别是在极端条件下,如极低温下量子涨落越来越强时。实际操作中,人们在不同温区会利用不同原理设计的温度计,像电阻噪声热温度计和磁热温度计。
发光效率
Kcd 是频率为540×10 12 赫兹的单色辐射光源在某个方向的辐射强度,为1/683瓦特每球面度,是衡量光源产生可见光能力的指标,它的发光强度为1坎德拉。1坎德拉的点状光源的总光通量为4π流明。1瓦白炽灯的发光强度约为1坎德拉。与通常的测量能量强度相比,发光强度的定义考虑了人的视觉因素和光学特点。这个量的选择明显带有人为因素,和其他几个基本常数相比,有本质差别,它并不是出现在物理方程中的常数。笔者相信这个量是可以用量化来定义的,例如以单位时间每球面度某个频率的光子抵达的数目来定义,像前面用基本电荷e来定义电流单位安培一样。随着激光和量子信息技术的发展,人们会对和量子光学相关的课题有更深入的理解,可能会有更好的亮度标准出现。
至于阿伏加德罗常数
NA ,它是用于标准化样品中以摩尔为单位的归一化因子。这个数以前是质量为12克的碳-12中原子的数目。这个量现在是国际单位制中的定义常数。虽然阿伏加德罗常数NA曾在科学发展过程中起到了积极作用,但现在它更多的是承接科学发展的连贯性。在凝聚态物理深入发展的今天,我们对微观世界有了更深刻的认识,这个常数的重要性可能会逐渐减弱,至少在凝聚态物理这个领域,早已没有这个常数的痕迹了。
10结 语
国际标准单位制还在不断进步和完善,以提高我们的测量精度。从实物原器到物理常数的转化,提高了它的普适性、科学性和代表性。严格地说,铯原子基本频率标准Δ
Cs 没有完全摆脱实物标准,并不是一个最基本的物理常数。以铯原子为基础的基本频率标准正接受新的挑战,现在已有一些新的系统,如核钟或核光钟,将使用核异构体跃迁的能量作为参考频率,可以达到更高的精度,并且更加稳定,这个技术最近有重大的突破 [4] 。相信在不久的将来铯原子的基本频率标准可能会被核钟取代,以提高时间的测量精度。
尽管国际标准单位制有着非常坚实的科学基础,在科学领域已被广泛接受和应用,但在不同国家和地区的日常生活和商业交流中并没有被完全接受。例如,英制仍然在一些地方广泛应用,不同行业仍保持各自的习惯。在香港的街市中,人们仍在使用司马斤(十六两制/0.6048千克),而在超市中,公斤和磅被混杂使用。一般内地城市市斤被广泛使用(十两制/0.500千克),而在新疆和云南昆明周边的集市上使用的是公斤(1.000千克),这说明要改变生活习俗是很难的。推广统一的度量衡单位仍然面临着艰巨的挑战,不过这已不是科学范畴的事情了。
最后再回到文章的原题:一米有多长,一公斤有多重?答案是:
一米的长度等于光速除以铯原子的频率乘以9192631770再除以299792458。
一公斤的质量等于普朗克常数乘以铯原子的频率,再除以光速的平方,然后乘以1.42118845813×1040。这个答案充分体现了现代科学对质量的精确定义和测量。
致 谢感谢牛谦教授在成文过程中的深入讨论。
参考文献
[1] Wikipedea:International System of Units/本文中引用的有关数据主要来自维基百科中的相关条目
[2] Newell D B. Physics Today,2014,67(7):35
[3] 张伟阳,董翔宇,王少凯 . 物理,2024,53(12):820
[4] Gibney E. Nature,2024,636:544
《物理》50年精选文章
方道配资提示:文章来自网络,不代表本站观点。